Cálculo de los esfuerzos máximos de la sección de hormigón armado a flexión y axil. Generación del diagrama interacción, tanto según el diagrama parábola rectángulo como según el diagrama rectangular del hormigón, y del diagrama de dominios de deformación, según EHE-08.

• El diagrama de interacción de la sección de hormigón está desarrollado según la EHE-08, con el comportamiento del hormigón especificado en el articulo 39.5, siguiendo tanto el diagrama parábola rectángulo como el diagrama rectangular de tensión-deformación de cálculo del hormigón. En este diagrama de interacción, la combinación de máximos axiles y momentos de la sección se obtiene a partir de las deformaciones maximas que admite la sección según el diagrama de dominios de deformación descrito en el artículo 42.
  
  
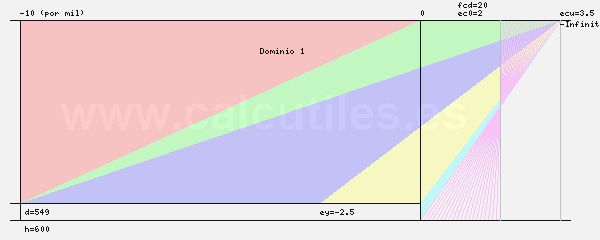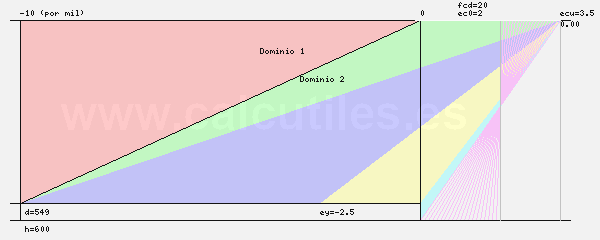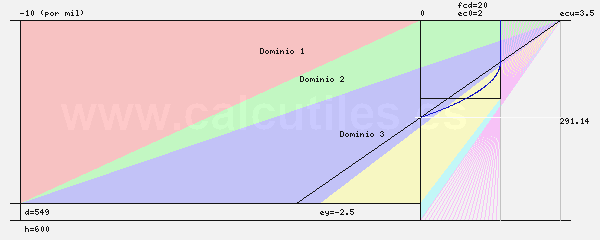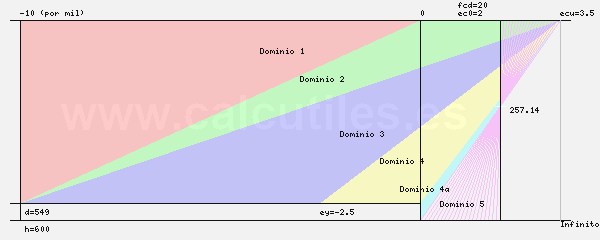
• El diagrama de dominios de deformación se genera a partir de las máximas deformaciones admisibles del hormigón y del acero, al considerar el eje neutro desplazándose desde el -∞ hasta el +∞.
  
  
• El diagrama de interacción se ha obtenido calculando en cada posición del eje neutro, el equilibrio de fuerzas y de momentos respecto al punto medio de la sección de hormigón.
  
  
• Las fuerzas y momentos de las armaduras se calculan sumando las de cada barra de acero. Las fuerzas y momentos del hormigón se calculan según el bloque de hormigón comprimido a partir del diagrama parábola rectángulo, y del diagrama rectangular.
  
  
• El diagrama de dominios de deformación es el siguiente:
  
  
  
  

Parámetros:
Materiales:
Hormigón: fck =	.2530354045 505560708090100.	N/mm2
Minoración hormigón Yc =				Yc = 1.5 excepto en situación accidental (Yc = 1.3), fatiga o fuego (EHE-08, 15.3)
Factor de cansancio a compresión αcc =		(*1)		En general αcc = 1 (en EHE-98 αcc = 0.85)
Acero: fyk =	.400500.	N/mm2		Ys = 1.15 excepto en situación accidental (Ys = 1.0), o control intenso (Ys = 1.10)(ver EHE-08, 15.3)
Minoración acero Ys =
Módulo de elasticidad del acero Es =		N/mm2		Habitualmente Es = 200.000 N/mm2 (EHE-08, art. 38.8 y comentarios en art. 38.4)
Sección:
Ancho (máx. 2000) =		mm
Canto (máx. 2000) =		mm
Recubrimiento nominal superior =		mm
Recubrimiento nominal inferior y laterales =		mm
Armado:
Cerco: ø =	.No hay681012 1416202532 40.	mm(*2)
Armado superior:		ø	.681012 1416202532 40.	mm
Armado inferior:		ø	.681012 1416202532 40.	mm
Armado lateral (por cara):		ø	.681012 1416202532 40.	mm(*3)
Punto de comprobación:
Profundidad del eje neutro:		mm		(Para obtener resultados de un punto concreto de las gráficas)
Dibujar diagrama parábola-rectángulo:	Sí
Dibujar diagrama rectangular:	Sí
(*1)El factor de cansancio tiene en cuenta éste efecto en el hormigón, cuando está sometido a altos niveles de compresión debido a cargas de larga duración. En general se adopta αcc = 1, aunque el autor del proyecto debe valorar su reducción hasta 0.85, si la relación entre las cargas permanentes y las totales es alta, o en función de las características de la estructura (EHE-08, 39.4).
(*2)La norma permite reducir el radio de doblado en cercos o estribos de diámetro menor o igual a 12 mm, con lo que es recomendable no utilizar cercos de mayores diámetros, siendo preferible colocar cercos dobles o triples en caso de ser necesario. (EHE-08, 69.3.4).
(*3)El armado lateral introducido se considera en el cálculo. Si no quiere considerarlo resistente por destinar su capacidad mecánica para flexiones horizontales, o por cualquier otro motivo, no debe introducirlo en el programa. No obstante, debe verificarse que se cumplen las separaciones de armaduras especificadas en la normativa (puede emplearse la utilidad "Árido y separaciones")
		Cálculo sin limitaciones para los usuarios con subscripción activa. (+info)

Resultados:
Materiales:
Deformación elástica del acero =	2.5	‰
Resistencia a compresión del hormigón fcd =	20	N/mm2		(EHE-08, 39.4)
Deformación de rotura a compresión simple εc0 =	2	‰		(EHE-08, 39.5)
Deformación última a flexión εcu =	3.5	‰		(EHE-08, 39.5)
Diagrama parábola-rectángulo del hormigón:
Grado de la parábola n =	2			(EHE-08, 39.5)
Máxima tracción =	-699.35	kN, con	0	mkN
Máximo momento en flexión simple =	Valor visible sólo para usuarios con subscripción activa. (+info)
Máximo momento combinado con axil =	522.95	mkN	2183.16	kN
Máxima compresión =	5443.4	kN, con	0	mkN
Diagrama rectangular del hormigón:
η =	1			(EHE-08, 39.5)
λ =	0.8			(EHE-08, 39.5)
En punto de comprobación: η(50) =	1			(EHE-08, 39.5)
En punto de comprobación: λ(50) =	0.07			(EHE-08, 39.5)
En punto de comprobación: área rectángulo(50) =	0.8	kN/mm		(EHE-08, 39.5)	A = [λ(50) * h] * [η(50) * fcd]
En punto de comprobación: Fuerza(50) =	320	kN		(EHE-08, 39.5)	F = A * b
En punto de comprobación: Momento(50) =	89.6	mkN
Máxima tracción =	-699.35	kN, con	0	mkN
Máximo momento en flexión simple =	Valor visible sólo para usuarios con subscripción activa. (+info)
Máximo momento combinado con axil =	530.46	mkN	2157.47	kN
Máxima compresión =	5443.39	kN, con	0	mkN
Diagrama de interacción:

• Estos cálculos propuestos por la normativa son muy precisos e instructivos, pero, en opinión del autor, su precisión se disuelve en la práctica al dimensionar los elementos con coeficientes de mayoración de acciones de un orden de magnitud tan elevado como los actuales de 1.35 y 1.5.
  
  
• En secciones de hormigón con recubrimientos o armado no simétricos, no se alcanza el equilibrio en tracción y compresión puras, apareciendo momentos en los valores de axiles extremos.
  
  
• Aunque en la EHE 08 el factor de cansancio se ha incrementado en torno a un 17% respecto a la EHE 98 (de 0.85 a 1), los esfuerzos máximos resistentes de la sección no se incrementan es este porcentaje, sino en porcentajes muy inferiores. De hecho se ha observado que en algún caso se reduce el esfuerzo máximo resistente a tracción, y el momento máximo en flexión simple. Con esto parece que efectuar los cálculos con el factor de cansancio según EHE-98 no queda en todos los casos del lado de la seguridad.
  
  

Versión 15/11/2012